試行錯誤が、子どもの可能性を拡げる

こんにちは、学びスタジオ®︎代表の奧川えつひろです。

ご訪問いただき、ありがとうございます。

今回は、試行錯誤について書きます。

❤︎試行錯誤は考える力

試行錯誤することが、

考える力を養います。

試行錯誤は、

ものごとを考える時に、

誰もが普通に行っていることです。

❤︎試行錯誤はPDCAサイクル

試行錯誤は、
自分なりの仮説を立てて、

実行してみて、

検証する。

いわゆる

ＰＤＣＡ（プラン・ドゥ・チェック・アクション）サイクルです。

❤︎中学受験の問題に試行錯誤

中学受験の問題は、

小学生の子どもにとっては、

試行錯誤するのにぴったりの教材です。

❤︎問題❶

例えば、

次のような問題考えてみます。

1＋2＋3＋4＋5＋6＋7＋8＋9＝？

もちろん、

順番に足していっても、

答えは出ます。

けれども、

単純に足していく以外にも計算のやり方はないか、

と問いかければ、

試行錯誤が始まります。

❶試行錯誤1

数式を見て（1・9）（2・8）・・・

と足して10になるセットを見つける子どもがいます。

❷試行錯誤2

あるいは、

1を5－4、9を5＋4、2を5－3、8を5＋3と考えて、

結局5が9つあると考える子どももいるかもしれません。

❸試行錯誤3

または、
　　1+2+3+4+5+6+7+8+9
＋）9+8+7+6+5+4+3+2+1

と考えて、10×9÷2＝45と答えを出すこともあり得るでしょう。

❤︎試行錯誤で大切なこと

❶何らかの見通しを持って試行錯誤する

大切なことは、

何らかの見通しを持った上で、

試行錯誤することであり、

これが考えることなのです。

❷「なぜ？」「どうして？」を投げ出さずに考えられる

また、

粘り強く、

最後まで投げ出さないで

試行錯誤することです。

❤︎問題❷

次は、魔法陣の問題です。

正方形型の9つのマスに、1から9までの数字を一回だけ使い、タテ・ヨコ・ナナメに並ぶ3つの数の和が同じになるように、数字を入れる問題です。

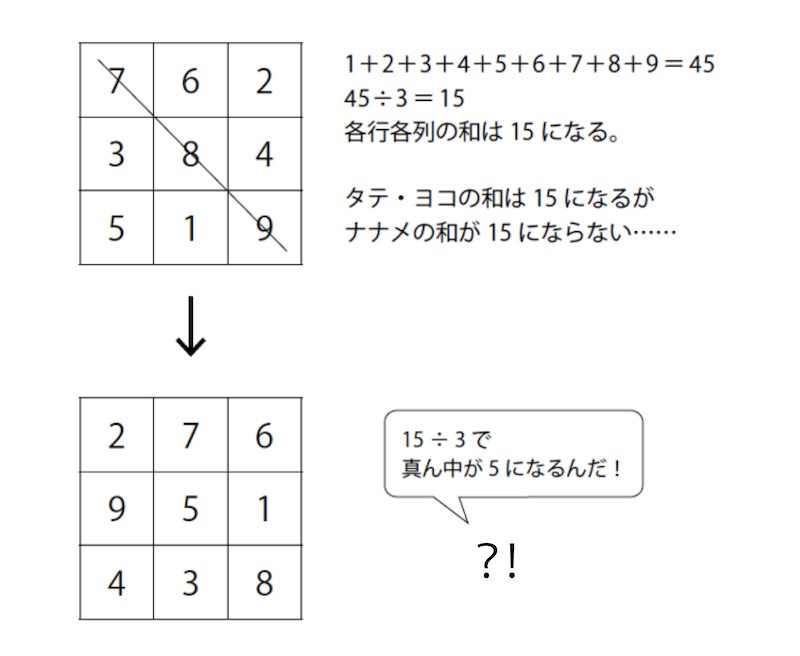
❶試行錯誤1

どこか端の数字を決めてしまったらどうなる

❷試行錯誤2

各行各列の和が１５になるのは、なぜか

❸試行錯誤3
真ん中の数か５でなければいけないのは、なぜか

当てずっぽうではなく、

何らかの見通しを立てて、

試行錯誤しながら考えていく。

これは算数に限らず、

いわゆる理系科目全般に共通する考え方です。

❤︎理科への効果

算数を通じて考える力を身につけたなら、
同じ理系科目の理科も

自然とわかるようになります。

物理の分野は、

テコ、滑車、バネ、浮力、電気などは、

考える力をつけるための良い材料となります。

生物分野は、

それこそ「なぜ？」「どうして？」と

不思議に思うことがいくらでもあるでしょう。

化学や地学は、

考える力を身につけた子どもにとっては、

自分で考えるネタの宝庫みたいなものです。

考える力をしっかり養っておけば、

小学校はもちろん、

中学校、高校と進んでも、

理系は得意科目となります。

❤︎国語への効果

算数の複雑な文章題を解くカギは、

まず問題の意味を理解することです。

つまり、

物事を筋道を立てて考える力がつけば、

文章を読んで理解することができるようになります。

文章を読んで理解することは、

文章として書かれている情報を整理することです。

もちろん、
算数の文章問題と国語の長文問題を比べれば、

文字数は圧倒的に国語の長文問題の方が多くなります。

しかし、

国語の長い文章も、

短い文がいくつも集まって構成されています。

だから、

一文一文を読んで、

書かれている内容を整理していけば、

長い文章の理解もしやすくなります。

後は、

長い文章に慣れる練習をしていけばいいのですね。

❤︎英語への効果

英語の場合、リーディングとライティングは、

ものごとを筋道立てて考える力があれば、

理解が速くなります。

なぜなら、

英語は日本語よりも、

文章の構造（文法）が

一定の法則によって決められています。

基本的な構成を見極めることができれば、

単語の意味がわかるかどうかです。

❤︎社会への効果

社会を学ぶ時に大切なのは、

年号や土地の名前、

人物などを覚えることですが、
「なぜ？」と「どうして？」から入っていくと、

理解しやすく、

理解したことなら覚えやすくなります。

歴史上のほぼすべての出来事は、

人によって起こされています。

人が行動する背景には、

それも何か歴史的な出来事が起こる際には、

必ず理由があるはずです。

であるならば、
その理由を考えることができるはずです。

いつ、どこで、何が、どのように起こったのかは歴史的な事実であり、

その時、最も大切なのが、

誰が「なぜ」そのような行動を起こしたのかです。

❤︎まとめ。試行錯誤が相乗効果をもたらす

中学受験の算数の文章問題には、

試行錯誤する要素がいっぱい詰まっています。

それをを解く子どもたちは、
文章を理解することから始まり、
次に、試行錯誤しながら、
問題に向き合うことになります。

見通しを立て、

答えが出るまで粘り強く試行錯誤します。
試行錯誤して問題を考えた結果、
正しい答えを導き出せる場合もあれば、
導き出せない場合もあると思います。

例え、

正しい答えが導き出せなくても、
考える力は、

確実についていきます。

この"試行錯誤"して学ぶ姿勢の中に、
子どものたくさんの可能性が詰まっています。